Cant Miss Takeaways Of Info About How Many 2x1 MUX Required To Design 16x1
Design 16*1 Mux Using 4*1
Unlocking the Secrets of Multiplexers
1. The Multiplexer Maze
Ever wondered how computers juggle so many different signals at once? The unsung hero is often the multiplexer, or MUX for short. Think of it as a tiny traffic controller for data. Now, we're not talking about the kind of traffic that gets you stuck on the highway (thankfully!), but rather electronic signals zipping around inside your devices. And today's puzzle? Figuring out how many of those handy 2x1 MUXes you need to build a beefier 16x1 MUX. It's not as daunting as it sounds, I promise!
A 2x1 MUX is the simplest form. It has two inputs, one select line (which acts like the switch), and one output. Based on the select line's value (either 0 or 1), one of the two inputs is passed through to the output. Pretty straightforward, right? The select line is the key. It decides which input gets the spotlight.
Now, a 16x1 MUX is a bit more ambitious. It has 16 inputs and, you guessed it, one output. To select one of the 16 inputs, you need more than a single select line. In fact, you'll need four (since 24 = 16). Each combination of these four select lines will correspond to one of the 16 inputs, determining which one makes its way to the output. It's like having 16 different doors, and you need four keys to unlock the specific door you want.
So, how do we combine these simple 2x1 MUXes to create our mighty 16x1? That's where the fun begins! We'll need to think about this in stages, like building a pyramid.
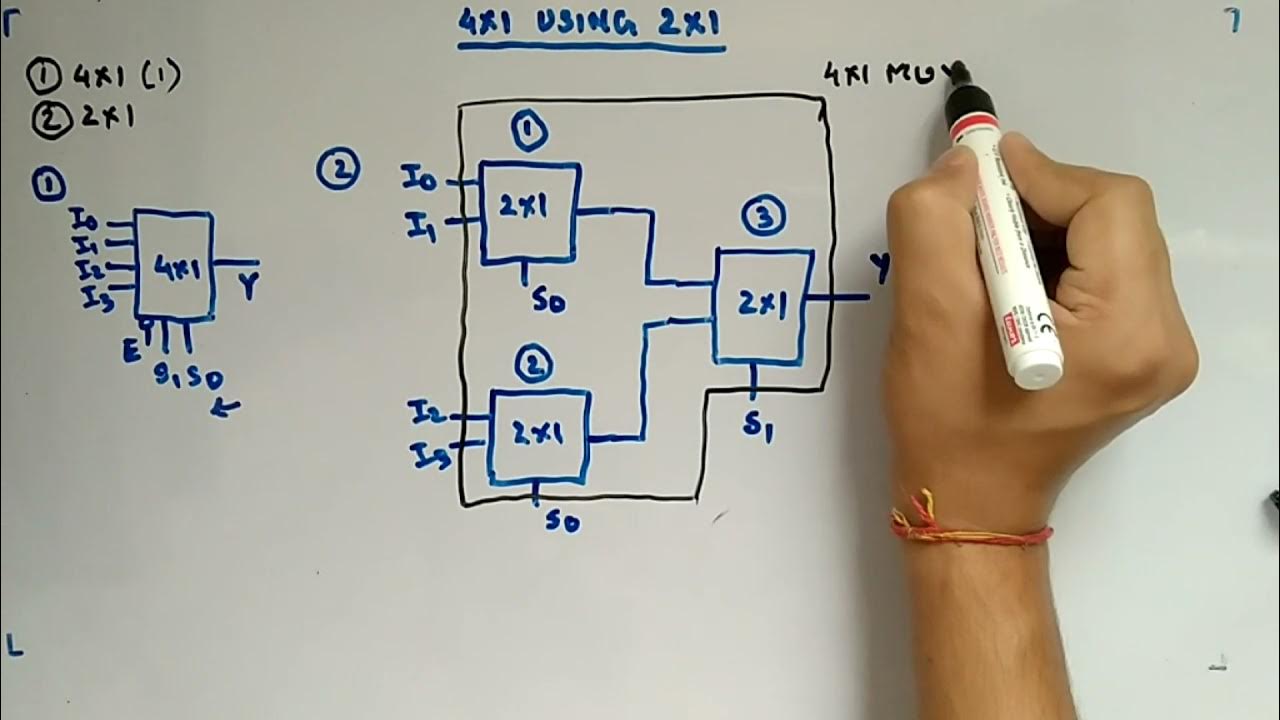
4x1 Using 2x1 Multiplexer Digital Circuits And Logic Design YouTube
Breaking Down the Build
2. The Power of Two
The secret to creating a 16x1 MUX from 2x1 MUXes lies in a hierarchical approach. Think of it like this: you wouldn't try to build a skyscraper all at once, would you? You'd start with the foundation and work your way up, one level at a time. The same principle applies here. We're going to break down the 16x1 MUX into smaller, more manageable chunks.
First, we'll use eight 2x1 MUXes to reduce the 16 inputs to 8. Each 2x1 MUX takes two inputs and selects one, effectively halving the number of signals we need to manage. Consider these eight MUXes as our first level of filtering. They're like eight pairs of contestants in a game show, and each MUX picks the winner from its pair.
Next, we'll take those eight outputs from the first stage and feed them into four more 2x1 MUXes. This reduces our number of inputs to four. We're essentially repeating the process, narrowing down the choices step by step. It's like a tournament bracket, where winners advance to the next round until only one champion remains.
Following this pattern, we then use two 2x1 MUXes to reduce the four inputs to two. And finally, one last 2x1 MUX selects between those final two inputs, giving us our single output. This final MUX is the ultimate gatekeeper, deciding which of the original 16 inputs gets to shine.
The Math Behind the MUX
3. Crunching the Numbers
Alright, let's get down to the brass tacks. How many 2x1 MUXes did we use in total? Remember, we used eight in the first stage, four in the second, two in the third, and one in the final stage. Adding those up, we get 8 + 4 + 2 + 1 = 15. So, the answer is 15! It takes fifteen 2x1 MUXes to create a single 16x1 MUX. Pretty neat, huh?
This hierarchical approach is efficient because it breaks down a complex problem into smaller, more manageable steps. It's a classic divide-and-conquer strategy, and it works wonders in digital logic design. You could use this same principle to build even larger MUXes. For example, building a 32x1 MUX would only require adding one more layer of 2x1 MUXes!
Another way to think about it is that for an n-to-1 MUX (where n is a power of 2), you need n-1 2x1 MUXes. So, for 16-to-1, 16-1=15. Simple! This formula comes from how the MUXes are structured in layers, halving the number of inputs at each stage.
If you're ever designing a digital circuit and need a larger MUX, remember this little trick. It'll save you a lot of time and effort compared to trying to build it from scratch. Plus, it's a great way to impress your friends with your newfound knowledge of multiplexer magic!

Digital Logic Block Diagram Of 161 MUX Using Four 41 Only
Beyond the Basics
4. MUXes in the Real World
Now that we know how to build a 16x1 MUX, let's talk about where you might actually find one in the wild. MUXes are used extensively in digital systems, from computers and communication networks to video games and medical equipment. They're the workhorses that enable us to share resources efficiently and make complex decisions with minimal hardware.
For example, in a computer's memory system, MUXes are used to select which memory location is being accessed. In communication systems, they allow multiple signals to be transmitted over a single channel. In video games, they might be used to select which texture to display on a 3D model. The possibilities are endless!
When designing with MUXes, it's essential to consider factors like propagation delay (how long it takes for the signal to pass through the MUX), power consumption, and cost. These factors will influence your choice of MUX technology (e.g., CMOS, TTL) and the overall performance of your system.
Another important consideration is the number of inputs and outputs you need. While we've focused on 2x1 and 16x1 MUXes, there are many other sizes available, such as 4x1, 8x1, and even larger. Choosing the right size MUX for your application can help optimize your design for performance and efficiency.

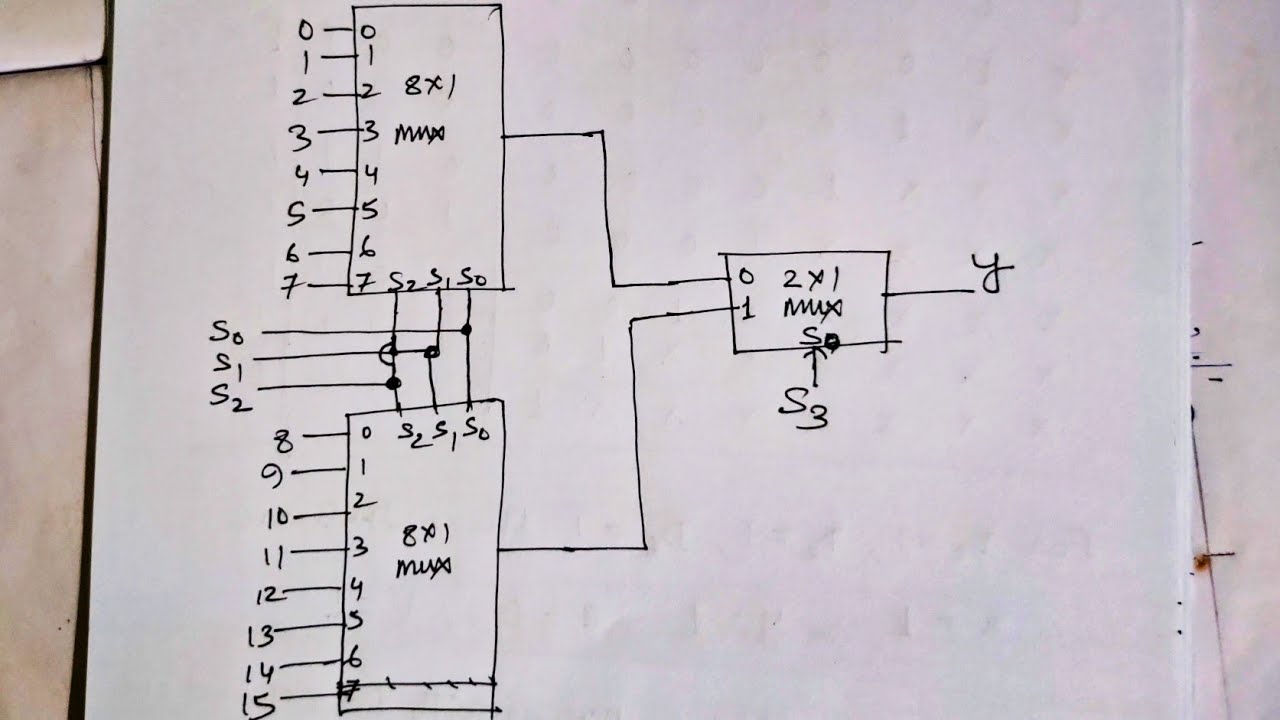
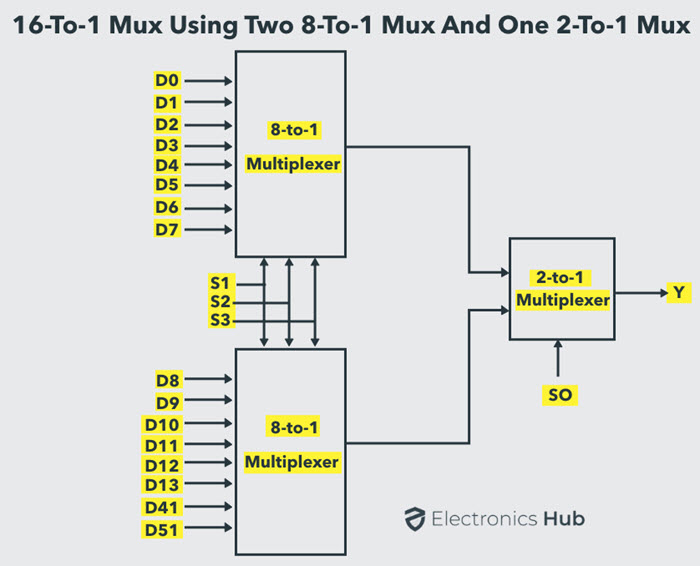
3.17 Design Of A 16x1 Multiplexer Using 8X1 Multiplexers, 4x1
MUX FAQs
5. Your Questions, Answered
Still scratching your head about multiplexers? No problem! Here are a few frequently asked questions to help clear things up:
Q: What's the difference between a MUX and a DEMUX?
A: A MUX (multiplexer) takes multiple inputs and selects one to pass through to the output. A DEMUX (demultiplexer) does the opposite: it takes a single input and directs it to one of multiple outputs. Think of a MUX as a funnel that combines multiple streams into one, and a DEMUX as a splitter that divides one stream into multiple.
Q: Can I use a MUX to reduce the number of wires in a circuit?
A: Absolutely! This is one of the primary applications of MUXes. By multiplexing multiple signals onto a single wire, you can significantly reduce the number of wires needed to transmit data. This is particularly useful in systems where wiring is expensive or space is limited.
Q: Are there different types of MUXes besides 2x1?
A: Yes! As mentioned earlier, there are MUXes with various numbers of inputs, such as 4x1, 8x1, 16x1, and so on. The size of the MUX depends on the number of inputs you need to select from. There are also analog MUXes, which can switch analog signals, and digital MUXes, which switch digital signals.
Q: What are the advantages of using MUXes?
A: Here's a quick rundown: MUXes simplify circuit designs, reduce the number of integrated circuit (IC) packages, and cut down on wiring complexity, which ultimately helps to minimize cost and space. They are particularly useful in complex logic designs where selective routing of data is crucial.
